2019 August 10 PyTorch

pytorch 101, part 1

原文地址，原文作者：Ayoosh Kathuria

翻译：zweien

Github 本文代码

预备知识

  1. 链式法则
  2. 对深度学习的基本理解
  3. PyTorch 1.0 +

自动微分 Automatic Differentiation

我们并不先从PyTorch的基本结构开始讲起，先来了解下每个深度学习框架必备的自动微分原理。

通过 PyTorch 的自动微分引擎 Autograd，有助于我们更好的理解自动微分的基本原理。

现代神经网络架构拥有数百万个可学习参数(learnable parameters)，从计算的角度来看，训练一个神经网络包括两个阶段：

  1. 一个前向过程（forward pass）用来计算损失函数（loss function）
  2. 一个反向过程（backward pass）用来计算损失函数关于可学习参数的导数

前向过程很好理解，一层神经网络的结果就是下一层的输入。

反向过程的理解稍显复杂，需要我们通过微积分中的链式法则来计损失函数关于可学习参数的导。

示例

首先我们考虑一个只包含5个神经元（neuron）的神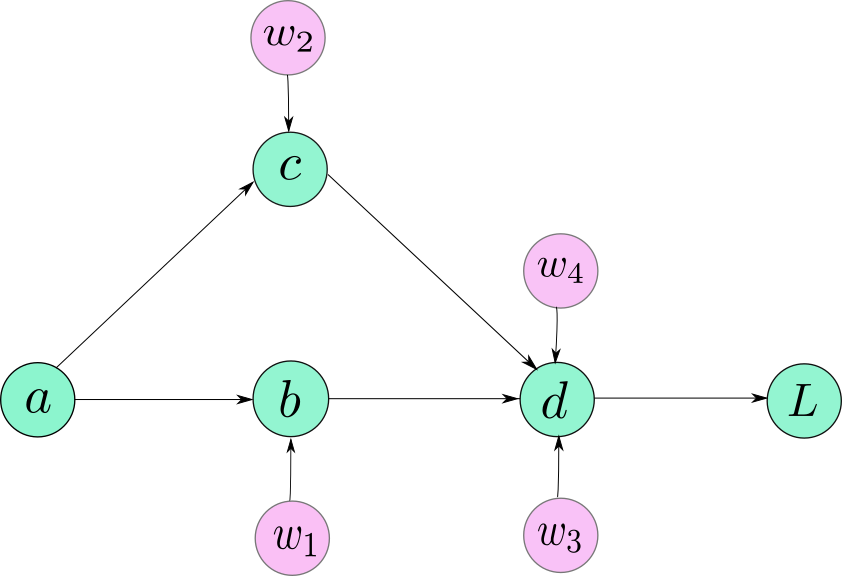经网络： 神经网络

该网络通过以下方程来描述：

\begin{aligned} b &=w_{1} * a \\ c &=w_{2} * a \\ d&= w_{3} * b+w_{4} * c \\ L &=10-d \end{aligned}

运用链式法则，我们计算下 $L$ 关于每个参数的导数

\begin{aligned} \frac{\partial L}{\partial w_{4}} &=\frac{\partial L}{\partial d} * \frac{\partial d}{\partial w_{4}} \\ \frac{\partial L}{\partial w_{3}} &=\frac{\partial L}{\partial d} * \frac{\partial d}{\partial w_{3}} \\ \frac{\partial L}{\partial w_{2}} &=\frac{\partial L}{\partial d} * \frac{\partial d}{\partial c} * \frac{\partial c}{\partial w_{2}} \\ \frac{\partial L}{\partial w_{1}} &=\frac{\partial L}{\partial d} * \frac{\partial d}{\partial b} * \frac{\partial b}{\partial w_{1}} \end{aligned}

计算图（Computational Graphs）

示例中的网络非常简单，所以我们能够很快的计算出每个导数。但是，如果网络的层数非常深，或者网络存在多个分支，这样的显示计算变得非常困难。

当我们开发软件来实现神经网络时，我们希望不管网络的构造如何，都能无缝的计算相应的梯度，这样当开发人员改变网络构造时也不用从新手动推导这些导数。

我们通过一种叫做计算图的数据结构来实现这一想法。计算图跟上文的示例中的网络图很像，不同点是，除了用户定义的变量外，计算图中的每个节点代表一个基本的运算符（operator）。

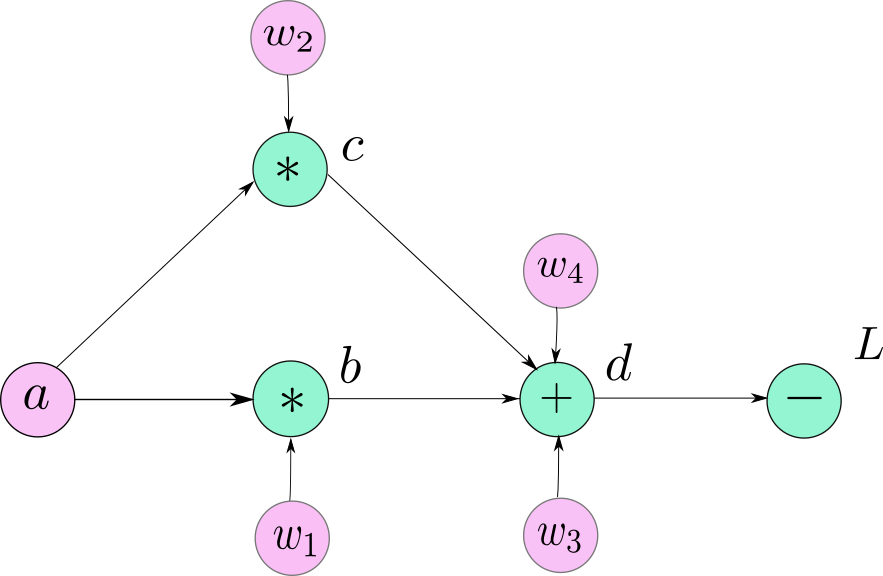计算图

其中变量 $b, c, d$ 表示数学运算的结果，变量 $a, w_1, w_2, w_3, w_4$ 由用户定义（叶节点 leaf node）。

计算梯度

下面开始利用计算图来计算梯度。

除了叶节点，计算图中的每个节点都能看成是包含输入输出的函数。来看一下输入 $w_4c、w_3b$ 输出 $d$ 的节点，可以写成 \(d=f\left(w_{3} b, w_{4} c\right)\)

$d$ 是函数 $f(x, y) = x + y$ 结果

我们能够计算出 $f$ 关于其输入的导数，$\frac{\partial f}{\partial w_{3} b}$、$\frac{\partial f}{\partial w_{4} c}$（都是 1），然后反向标记出相应导数

局部梯度

对整个计算图重复该操作

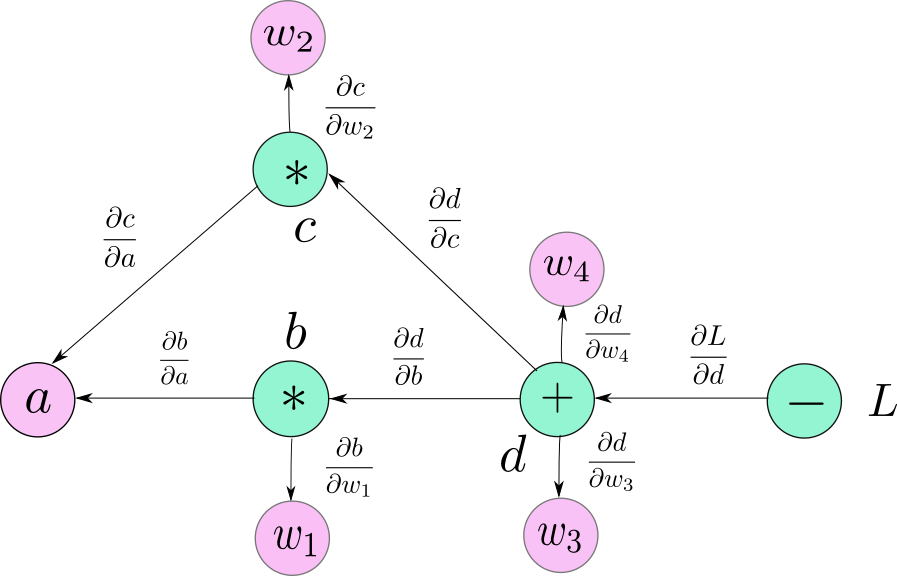反向传播

下面考虑损失函数 $L$ 关于任意节点的导数，例如考虑 $\frac{\partial L}{\partial a}$

  1. 找出从 $d$ 到 $w_4$ 的所有可能路径
  2. 从图中可以看到，有 2 条可能路径
  3. 对于每条路径，沿着路径将边上的所有值相乘
  4. 将每条路径的乘积相加
\[\frac{\partial f}{\partial a}=\frac{\partial L}{\partial d} * \frac{\partial d}{\partial b} * \frac{\partial b}{\partial a}+\frac{\partial L}{\partial d} * \frac{\partial d}{\partial c} * \frac{\partial c}{\partial a}\]

PyTorch Autograd

下面我们回到 PyTorch，看一下上述过程在 PyTorch 中如何实现。

张量（Tensor）

Tensor 是 PyTorch 中的基本数据结构，类似于 numpy 中的 ndarray，使用语法也与其相似，但却拥有在 GPU 上并行计算的能力。

In  [1]: import torch
In  [2]: tsr = torch.Tensor(3,5)  
In  [3]: tsr
Out [3]: tensor([[  0.0000e+00, 0.0000e+00, 8.4452e-29, -1.0842e-19, 1.2413e-35],
                 [  1.4013e-45, 1.2416e-35, 1.4013e-45, 2.3331e-35, 1.4013e-45],  [  1.0108e-36, 1.4013e-45, 8.3641e-37, 1.4013e-45, 1.0040e-36]])

如果想使用 PyTorch 建立计算图，只需要设置 Tensor 的参数 requires_grad 为 True。

>> t1 = torch.randn((3,3), requires_grad = True)
>> t2 = torch.FloatTensor(3,3) # 不在初始化中设置 requires_grad
>> t2.requires_grad = True

requires_grad 具有传递性，意味着当一个 Tensor 由其它 Tensor 导出，只要任意源头 Tensor 的 requires_grad 为 True，那么后续 Tensor 的 requires_grad 也为 True。

每个 Tensor 都有参数 grad_fn，用来表示导出该变量的运算符。如果 requires_grad 是 False 的话，grad_fn 将会是 None。

在我们的例子中，$d=f\left(w_{3} b, w_{4} c\right)$，$d$ 的 grad_fn 为加法运算，因为 $f$ 将其输入相加，注意到，加法操作符也是计算图中用来得到 $d$ 的节点。如果一个 Tensor 是叶节点的话（由用户初始化），那么 grad_fn 为 None。

import torch
a = torch.randn((3,3), requires_grad = True)
w1 = torch.randn((3,3), requires_grad = True)
w2 = torch.randn((3,3), requires_grad = True)
w3 = torch.randn((3,3), requires_grad = True)
w4 = torch.randn((3,3), requires_grad = True)
b = w1*a c = w2*a d = w3*b + w4*c L = 10 - d
print("The grad fn for a is", a.grad_fn)
print("The grad fn for d is", d.grad_fn)

运行上述程序，将会得到如下形式的输出

The grad fn for a is None
The grad fn for d is <AddBackward0 object at 0x1033afe48>

我们可以利用成员函数 is_leaf 来判断是否是叶节点。

函数 Function

PyTorch 中的所有数学运算符都由类 (class) torch.autograd.Function 来实现，该类中包含两个重要的成员函数。

第一个是静态函数 forward，用来实现从输入到输出这一过程。

第二个是静态函数 backward，用

还是通过例子 $d=f\left(w_{3} b, w_{4} c\right)$ 来理解。

  1. Tensor $d$ 的 grad_fn 是 AddBackward
  2. grad_fn 的 forward 接受输入 $w_3b、w_4c$，将他们相加，将结果存于 $d$
  3. ThAddBackward的 backward 函数接受从后续层中传来的导数，即 $\frac{\partial L}{\partial d}$，该导数存于 d.grad 中
  4. 计算局部导数$\frac{\partial d}{\partial w_{4} c}$ and $\frac{\partial d}{\partial w_{3} b}$
  5. 然后 backward 函数将上两步的结果相乘，然后将结果继续“传送”到 $f$ 的输入变量的 grad_fn的 backward。
  6. 举例来说， <AddBackward> 的 backward 将结果传递给 $w_{4} * c$ 的 grad_fn（这里 $w_{4} * c$ 是中间变量，其 grad_fn 是 <MulBackward>, 可有 d.grad_fn.next_functions 查看）。
  7. 对于$w_{4} * c$， 上一步计算得到的 $\frac{\partial L}{\partial d} * \frac{\partial d}{\partial w_{4} c}$ 将作为梯度输入。

上述过程可从以下程序来描述（并不是 PyTorch 中的实际实现）

def backward (incoming_gradients):
    self.Tensor.grad = incoming_gradients

    for inp in self.inputs:
        if inp.grad_fn is not None:
            new_incoming_gradients = //
              incoming_gradient * local_grad(self.Tensor, inp)
            
            inp.grad_fn.backward(new_incoming_gradients)
        else:
            pass

这里的 self.Tensor 由 autograd.Function 所创建，也就是上文例子中的 $d$

为了训练神经网络，我们需要计算损失函数关于参数的梯度，通过调用loss.backward 函数，利用 loss.grad_fn 沿计算图上的路径反向计算相应导数。

在反向传播中，backward 函数被迭代调用，当达到叶节点时，应为其 grad_fn 为 None，迭代过程终止。

还有一点需要注意的是，对向量 Tensor 直接调用 backward() 将会报错（译注：向量Tensor的调用参见官方文档torch.autograd.backward 部分）。通常来说我们针对标量 Tensor 来调用 backward，例如

import torch 

a = torch.randn((3,3), requires_grad = True)

w1 = torch.randn((3,3), requires_grad = True)
w2 = torch.randn((3,3), requires_grad = True)
w3 = torch.randn((3,3), requires_grad = True)
w4 = torch.randn((3,3), requires_grad = True)

b = w1*a 
c = w2*a

d = w3*b + w4*c 

L = (10 - d)

L.backward()

运行上述代码，将产生如下错误

RuntimeError: grad can be implicitly created only for scalar outputs

这是因为默认情况下，只能针对标量计算相应导数值。数学上，一个向量对另一个向量求导得到雅克比矩阵。

由两种方法来解决这种问题。

如果修改上述代码，将 L 改为误差之和，问题将被解决：

import torch 

a = torch.randn((3,3), requires_grad = True)

w1 = torch.randn((3,3), requires_grad = True)
w2 = torch.randn((3,3), requires_grad = True)
w3 = torch.randn((3,3), requires_grad = True)
w4 = torch.randn((3,3), requires_grad = True)

b = w1*a 
c = w2*a

d = w3*b + w4*c 

# Replace L = (10 - d) by 
L = (10 -d).sum()

L.backward()

执行过后，就可以通过相应变量的 grad 属性来访问相应导数。

另一种处理方式，我们也可以在调用向量值张量的backward时，显示的传入参数，其形状要和被调用的张量一致

# Replace L.backward() with 
L.backward(torch.ones(L.shape))

通过自动微分这一机制，我们就能实现优化算法中的导数计算，例如

w1 = w1 - learning_rate * w1.grad

动态计算图

PyTorch 使用了一种叫做动态计算图的机制，意味着计算图是在运算中建立的（on the fly）。

具体来说，直到运算符的 forward 被执行时，计算图才被建立。

a = torch.randn((3,3), requires_grad = True)   #No graph yet, as a is a leaf

w1 = torch.randn((3,3), requires_grad = True)  #Same logic as above

b = w1*a   #Graph with node `mulBackward` is created.

计算图将随着forward函数的执行被建立，此时生成对非叶节点、计算图、中间变量的缓存。 当执行backward时，相应导数将被计算，相应缓存(非叶节点)将被释放，并且计算图将被销毁（也就是所，我们将不能再次执行导数的反向传播，因为）

下一次，当对同一组张量执行 forward 时，叶节点的缓存将被共享，而非叶节点的缓存将再次建立。

如果对对非叶节点两次执行 backward，将得到以下错误

RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time.

这是因为非叶节点的缓存在第一次执行backward时就已经释放，第二次执行时无法找到执行backward的路径。值得注意的是，我们可以在执行backward时传入参数retrain_graph=True来取消这一机制，如

loss.backward(retain_graph = True)

这时，计算图中导数将反向传播两次，相应导数将累计，也就是说，第二次执行时，相应导数将与第一次得到导数相加。

这一动态计算图机制与静态计算图（Static Computation Graphs）不同，例如 TensorFlow。（译注：TensorFlow 已引入 Eager Execution 模式）

在静态计算图模式中，计算图必须在在实际运算前预先建立，然后在将数据传给（feed）计算图进行计算。

动态计算图允许我们在执行中动态的修改网络结构，因为计算图只是在部分代码运行时才会被建立，对于静态计算图来说，这一功能就无法实现。

动态计算图同时也更易于调试。

一些 Tricks

requires_grad

requires_grad是Tensor类的属性，默认为 False。在训练过程中，当需要固定网络某些层的参数时，可以将那些层的参数的requires_grad属性设置为False，这样这些参数将不会参与相应的反向传播。

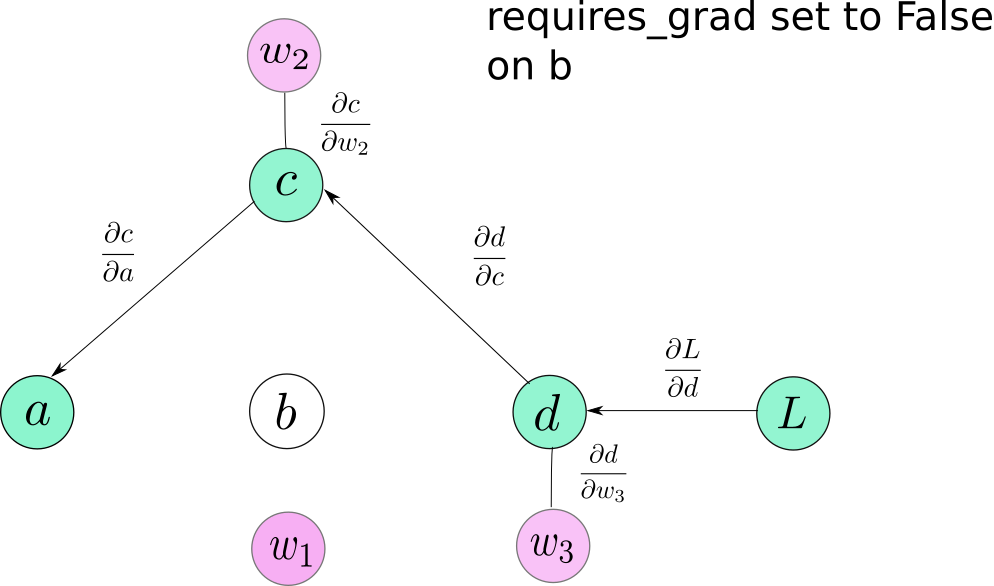
这样，相应导数将不会被传递，同时该参数之前的参数也不会参与进来。

torch.no_grad()

当我们计算梯度时，我们对运算的输入、中间值进行缓存，因为在导数反向传播我们需要这些值。

然而，当我们进行推断（inference）时，我们并不需要计算相应的梯度，所以我们并不需要存储这些值。事实上，并不需要建立相应计算图，这样便可以节省内存消耗。

出于该目的，PyTorch 提供了上下文管理器(context manager) torch.no_grad

with torch.no_grad:
    inference code goes here

这样，中间过程执行中将不会建立计算图。

结论

理解自动微分与计算图的工作原理将有助于我们 PyTorch 的学习与使用。掌握这一基础后，下篇博文将介绍复杂结构的建立、自定义数据流和更多有趣的内容。

进一步阅读

  1. Chain Rule
  2. Backpropagation

All content is licensed under CC BY-NC-SA

Built with Jekyll and 3-Jekyll theme • Hosted on Github

Table of Contents